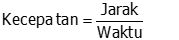10 Contoh Soal Kecepatan, Jarak, dan Waktu

Berikut ini akan kami sampaikan soal-soal yang berkaitan dengan jarak kecepatan dan waktu. Nah bagaimana cara penyelesiannya ? Simak materi berikut.

 1. Sebuah kendaraan melaju dari kota A menuju kota B selama 3 jam. Kendaraan tersebut melaju dengan kecepatan 50 km/jam. Berapa kilometer jarak antara kota A dengan kota B?

A. 145 km

B. 150 km

C. 155 km

D. 160 km

Jawaban: B

Jarak = Kecepatan × Waktu

         = 50 × 3

         = 150 km

Jadi, jarak antara kota A dan B adalah 150 km.

 

2. Dari rumah ke pantai berjarak 10 km, pada hari Minggu, Rudi dan temannya bermain naik sepeda dengan kecepatan 4 km/jam. Berapa jam Rudi dan temannya naik sepeda dari rumah sampai di pantai?

A. 2 jam 15 menit

B. 2 jam 30 menit

C. 2 jam 45 menit

D. 2 jam 55 menit

Jawaban: B

          = 2,5 jam

          = 2 jam 30 menit

Jadi, lama waktu naik sepeda dari rumah sampai pantai 2 jam 30 menit.

 

3. Sebuah kereta melaju dari Jakarta menuju Bandung selama 3 jam. Jarak antara Jakarta Bandung kurang lebih 240 km. Berapa km/jam kecepatan kereta tersebut?

A. 50 km/jam

B. 60 km/jam

C. 70 km/jam

D. 80 km/jam

Jawaban: D

  

               = 80 km/jam

Jadi, kecepatan kereta adalah 80 km/jam.

 

4. Sebuah kendaraan melaju dari kota A menuju kota B dengan kecepatan 90 km/jam. Jarak antara kota A dan kota B 315 km. Kendaraan tersebut berangkat pukul 09.30 pagi. Pukul berapa kendaraan tersebut tiba di kota B?

A. 11.00

B. 12.00

C. 13.00

D. 14.00

Jawaban: C

          = 3,5 jam

          = 3 jam 30 menit

3 jam 30 menit setelah pukul 09.30 menit dihitung sebagai berikut.

   09.30

     3.30 +

   13.00   (atau pukul 01 siang)

Jadi, kendaraan tersebut tiba di kota B pada pukul 13.00.

 

5. Pak Hendra mengendarai mobilnya ke Garut dengan kecepatan 40 km/jam. Jika ia memerlukan waktu 2 jam untuk tiba di Garut, berapakah jarak yang ditempuh?

A. 80 km

B. 85 km

C. 90 km

D. 95 km

Jawaban: A

Jarak = Kecepatan × Waktu

        = 40 × 2

        = 80 km

Jadi, jarak yang ditempuh adalah 80 km.

 

6. Bus melaju dari kota Solo menuju kota Semarang berangkat pukul 07.30 dan tiba pukul 09.30. Bus tersebut melaju dengan kecepatan 60 km/jam. Berapa kilometer jarak antara kota Solo dengan kota Semarang?

A. 100 km

B. 110 km

C. 120 km

D. 130 km

Jawaban: C

Lama waktu perjalanan dari pukul 07.30 sampai 09.30 adalah 2 jam.

Jarak = Kecepatan × Waktu

        = 60 × 2

        = 120 km

Jadi, jarak antara kota Solo dan Semarang adalah 120 km.

 

7. Sebuah kereta melaju dari Surabaya menuju Malang selama 2 jam. Jarak antara Surabaya Malang kurang lebih 180 km. Berapa km/jam kecepatan kereta tersebut?

A. 80 km/jam

B. 90 km/jam

C. 100 km/jam

D. 110 km/jam

Jawaban: B

               = 90 km/jam

Jadi, kecepatan kereta adalah 90 km/jam.

 

8. Dari rumah ke mall berjarak 60 km. Pada hari Minggu, Tari dan temannya pergi naik motor dengan kecepatan 45 km/jam. Berapa jam Tari dan temannya naik motor untuk sampai di mall?

A. 1 jam 15 menit

B. 1 jam 20 menit

C. 1 jam 35 menit

D. 1 jam 40 menit

Jawaban: B

          = 1 jam 20 menit

Jadi, lama waktu naik motor adalah 1 jam 20 menit.

 

 

9. Bu Zainab mengendarai mobilnya ke Ngawi dengan kecepatan 50 km/jam. Jika ia memerlukan waktu 3 jam untuk tiba di Ngawi, berapakah jarak yang ditempuh?

A. 120 km

B. 150 km

C. 180 km

D. 240 km

Jawaban: B

Jarak = Kecepatan × Waktu

        = 50 × 3

        = 150

Jadi, jarak yang ditempuh adalah 150 km.

 

10. Sebuah mini bus melaju dari kota C menuju kota D dengan kecepatan 60 km/jam. Jarak antara kota C dan kota D 270 km. Mini bus tersebut berangkat pukul 07.30 pagi. Pukul berapa kendaraan tersebut tiba di kota D?

A. 11.00

B. 12.00

C. 13.00

D. 14.00

Jawaban: D

          = 4,5 jam

          = 4 jam 30 menit

4 jam 30 menit setelah pukul 07.30 menit dihitung sebagai berikut.

   07.30

     4.30 +

   14.00   (atau pukul 02 siang)

Jadi, kendaraan tersebut tiba di kota D pada pukul 14.00.

 

 

SOAL LATIHAN

1. Angga dengan mengendarai sebuah sepeda motor dapat menempuh jarak 110 km dalam waktu 2,5 jam. Berapa km kecepatan rata-ratanya dalam setiap jam? Pembahasan:

 

2. Ahmad bersepeda dari Jogja ke Kasongan yang jaraknya 21 km dengan kecepatan rata-rata 10 km/jam. Ahmad beristirahat di perjalanan selama 15 menit. Jika Ahmad tiba di Kasongan pukul 09.00, pukul berapa ia berangkat?

 

3. Jarak tempat tinggal dan kampung halaman Farida adalah 200 km. Jika Farida naik mobil dengan kecepatan 40 km/jam dan berangkat pukul 17.30 WIB kemudian berhenti di jalan sebanyak 2 kali selama 15 menit, pukul berapa Farida sampai di kampungnya?

 

4. Balgis melakukan perjalanan dari kota A menuju kota C melalui kota B. Dari kota A ke kota B berangkat pada pukul 22.00 WIB, dengan kecepatan 100 km/jam sampai di kota B pukul 00.45 wib.

Di kota B, Balgis beristirahat selama 4 jam 30 menit dan langsung melanjutkan perjalanan ke kota C dengan kecepatan yang sama. Balgis sampai di kota C pada pukul 10.35 wib. Berapa km jarak kota A ke C?

 

5. Kendaraan berangkat dari kota Solo pukul 07.10 menuju kota Malang yang jaraknya 360 km. Kendaraan tiba di Malang pukul 10.50. Hitung kecepatan rata-rata kendaraan tersebut.

Demikian beberapa contoh soal tentang kecepatan dan waktu/

Semoga bermanfaat.

KUMPULAN SOAL ARITMETIKA SOSIAL DALAM PERBANKAN DAN KOPERASI

Dalam dunia perbankan pada umumnya tentang besar tabungan, suku bunga, angsuran, lama waktu menabung, tabungan awal, dan besarnya tabungan akhir.

Rumus-rumu

 

Tabungan akhir = Tabungan awal + Bunga bank

Bunga Bank = persentase bunga bank × besar tabungan awal

 

Yuk, simak beberapa soal tentang perbankan berikut!

 

Soal 1

Ridwan menabung di bank dengan besar tabungan besar tabungan awal

Rp1.200.000,00, suku bunga tabungan 9% per tahun. Ketika ia mengambil seluruh uang tabungannya, jumlah tabungan Ridwan menjadi sebesar Rp1.281.000,00. Lama Ridwan menabung adalah...

A. 6 bulan

B. 8 bulan

C. 9 bulan

D. 10 bulan

Jawaban: C

Tabungan Awal = TA = Rp1.200.000,00

Tabungan Akhir = TK = Rp1.281.000,00

Bunga bank = b = Rp1.281.000,00 – Rp1.200.000,00

                        = Rp81.000,00

Soal 2

Fajar menabung di sebuah bank sebesar Rp2.000.000,00. Setelah sembilan bulan tabungan Fajar menjadi Rp2.180.000,00. Besar suku bunga yang ditetapkan bank pertahun adalah...

A. 9 %

B. 10 %

C. 11 %

D. 12 %

Jawaban: D

Tabungan Awal = TA = Rp2.000.000,00

Tabungan Akhir = TK = Rp2.180.000,00

Bunga bank = b = Rp2.180.000,00 – Rp2.000.000,00

                        = Rp180.000,00

Lama menabung = n = 9 bulan

Soal 3

Diana menabung di bank sebesar Rp8.000.000,00. Setelah 8 bulan uangnya diambil seluruhnya sebesar Rp8.800.000,00. Berapakah persentase suku bunga tabungan pertahun yang diberikan bank tersebut?

A. 10 %

B. 12 %

C. 15 %

D. 18 %

Jawaban: C

Tabungan Awal = TA = Rp8.000.000,00

Tabungan Akhir = TK = Rp8.800.000,00

Bunga bank = b = Rp8.800.000,00 – Rp8.000.000,00

                        = Rp800.000,00

Lama menabung = n = 8 bulan

Soal 4

Arman menabung di bank sebesar Rp800.000,00 dengan suku bunga 9

% setahun. Tabungan Arman saat diambil sebesar Rp920.000,00. Lama Arman menabung adalah...

A. 18 bulan

B. 20 bulan

C. 22 bulan

D. 24 bulan

Jawaban: B

Tabungan Awal = TA = Rp800.000,00

Tabungan Akhir = TK = Rp920.000,00

Bunga bank = b = Rp920.000,00 – Rp800.000,00

                        = Rp120.000,00

Persentase bunga = %b = 9%

Soal 5

Setelah 9 bulan uang tabungan Winna di koperasi berjumlah Rp3.815.000,00. Koperasi memberi jasa simpanan berupa bunga 12% per tahun. Tabungan awal Winna di koperasi adalah . . . .

A. Rp3.500.000,00

B. Rp3.550.000,00

C. Rp3.600.000,00

D. Rp3.650.000,00

Jawaban: A

Tabungan Awal = TA = ?

Tabungan Akhir = TK = Rp3.815.000,00

Bunga bank = b = Rp3.815.000,00 – TA

Persentase bunga = %b = 12%

Lama waktu = n = 9

Soal 6

Pak Himawan menyimpan uangnya di bank sebesar Rp750.000,00 dengan bunga 18% per tahun. Besar uang Pak Himawan setelah 4 bulan adalah . . . .

A. Rp885.000,00

B. Rp880.000,00

C. Rp795.000,00

D. Rp761.250,00

Jawaban: C

Tabungan Awal = TA = Rp750.000,00

Tabungan Akhir = TK = ?

Persentase bunga = %b = 18%

Lama waktu = n = 4

TK = TA + bunga

     = 750.000 + 45.000

     = 795.000

Jadi, tabungan akhir adalah Rp795.000,00.

Soal 7

Untuk modal berjualan, Bu Endah meminjam uang di koperasi sebesar Rp6.000.000,00 dengan bunga 5% pertahun. Angsuran tiap bulan yang harus dibayar Bu Endah jika meminjam selama 10 bulan adalah . . . .

A. Rp440.000,00

B. Rp450.000,00

C. Rp550.000,00

D. Rp560.000,00

Jawaban:

Pinjaman Awal = PA = Rp6.000.000,00

Bunga pinjaman pertahun = b = 5%

Lama waktu = n = 10

= 5 × 5 × 10.000

= 250.000

Jumlah pinjaman yang harus dikembalikan

= Rp6.000.000,00 + Rp250.000,00

= Rp6.250.000,00

Besar angsuran perbulan (selama 10 bulan)

= Rp6.250.000,00 : 10

= Rp625.000,00

 Jadi, besar angsuran Bu Endah perbulan adalah Rp625.000,00

 

Demikian sedikit materi hitung perbankan yang dapat kami sampaikan semoga bermanfaat.

CONTOH SOAL TRIGONOMETRI JUMLAH DAN SELISIH DUA SUDUT

 Saat belajar trigonometri, jumlah dan selisih sudut menjadi salah satu materi yang dipelajari. Materi ini akan mempelajari rumus sinus, cosinus, dan tangen. Untuk memahaminya, contoh soal jumlah dan selisih dua sudut trigonometri dapat menjadi pembelajaran.

Dengan adanya contoh soal membuat lebih memahami materi tentang jumlah dan selisih dua sudut trigonometri. Di sisi lainnya, contoh soal membuat siswa tidak lagi kesulitan saat menemui soal yang serupa.

Peerhatikan rumus dasar trigonometri jumlah dan selisih dua sudut.

Sinus

Sin (A + B) = sin A cos B + cos A sin B

Sin (A - B) = sin A cos B - cos A sin B

Cosinus

Cos (A + B) = cos A cos B – sin A sin B

Cos (A - B) = cos A cos B + sin A sin B

Tangen

Perhatikan Contoh Soal berikut.

1. Tentukan nilai sin 150^o

Jawaban:

2. Tentukan nilai cos 160^o

Jawaban:

3. Tentukan nilai sin 255^o

Jawaban:

4. Tentukan nilai cos 195^o

Jawaban:

5. Tentukan nilai sin 285^o

Jawaban:

6. Tentukan nilai tan 75^o

Jawaban:

Demikianlah sedikit materi tentang trigonometri selisih dan jumah sudut.

Semoga Bermanfaat. 

SOAL SOAL YANG BERKAITAN DENGAN ARITMETIKA SOSIAL dan JUAL BELI (UNTUNG , RUGI, DISKON)

 

Pada kesempatan ini akan admin berikan beberapa contoh soal cerita berkaitan dengan aritmetika sosial. Aritmetika sosial merupakan materi yang mempelajari seluk beluk harga pembelian, harga penjualan, keuntungan, kerugian, persentase keutungan, persentase kerugian, bruto, tara, neto, dan pajak.

Nah, bagaimana bentuk soal aritmetika sosial dan pembahasannya?

Simak dan pelajari dibawah ini sampai kamu paham.

 

Soal 1

Pedagang buah apel fuji membeli dengan harga Rp20.000,00 per kg. Jka apel tersebut dijual dengan harga Rp25.000,00 per kg, maka hitung untung atau rugi pedagang tersebut? Jika untung, berapa keuntungannya? Dan jika rugi, berapa kerugiannya?

Pembahasan:

Harga pembelian Rp20.000,00

Harga penjualan Rp25.000,00

Tampak bahwa harga pembelian < harga penjualan

Rp20.000,00 < Rp25.000,00

Besar keuntungan

= harga jual - harga beli

= Rp25.000,00 - Rp20.000,00

= Rp5.000,00

Jadi, pedagang mendapatkan keuntungan sebesar Rp5.000,00,00.

 

Soal 2

Galih menjual roti dengan modal Rp80.000,00 dan hasil yang didapatkan dari penjualan roti adalah Rp100.000,00. Berapa persen keuntungan Galih?

Pembahasan:

Keuntungan = harga jual - moal

= Rp100.000,00 - Rp80.000,00

= Rp20.000,00

Persentase untung = untung/modal x 100% = 20.000,00/80.000,00 x 100%

= 1/4 x 100% = 25%

Jadi, keuntungan Galih 25%.

 

Soal 3

Seorang pedagang es keliling setiap hari mendapatkan keuntungan 30% atau Rp45.000,00. Hitunglah harga pembelian dan penjualannya!

Pembahasan:

Persentase untung = 30%

Pembelian = 100%/30% x 45.000

= 10/3 x 45.000

= 450.000/3

= 150.000

 

Penjualan = pembelian + untung

= Rp150.000,00 + Rp45.000,00

= Rp195.000,00

 

Jadi, harga pembelian Rp150.000,00 dan harga penjualan Rp195.000,00.

 

Soal 4

Pada sebuah kantong semen yang sering kita lihat terdapat tulisan netto 50 kg. Jika berat kantongnya 300 gram, berapa brutonya?

Pembahasan:

Netto = 50 kg

Tara = 300 gram = 0,3 kg

Bruto = Netto + Tara

         = 50 kg + 0,3 kg

         = 5,3 kg

Jadi, berat bruto semen adalah 5,3 kg

 

Soal 5

Satu lusin pulpen dibeli seharga Rp20.000,00. Setiap pulpen lalu dijual dengan harga Rp2.000 per buah. Jadi, berapa keuntungan yang bisa diperoleh dari penjualan 1 lusin pulpen tersebut?

Pembahasan:

Harga pembelian: Rp20.000,00

Harga penjualan: 12 x Rp2.000,00 = Rp24.000,00

Nilai keuntungan penjualan 1 lusin pulpen adalah:

Rp24.000,00 – Rp20.000,00 = Rp4.000,00.

 

Soal 6

Seorang pedagang es jus membeli 12 buah durian untuk bahan jualannya. Dia kemudian membayar pakai 3 lembar uang Rp100 ribuan, dan mendapatkan uang kembalian Rp30.000,00. Jika si pedagang itu hanya membeli 8 buah durian, dia harus membayarkan uang berapa?

Pembahasan:

Harga pembelian 12 buah durian adalah:

(3 × Rp100.000,00) – Rp30.000,00

= Rp300.000,00 – Rp30.000,00

= Rp270.000,00.

Harga pembelian durian per buah adalah: Rp270.000,00 / 12 = Rp22.500.

Harga pembelian 8 buah durian adalah:

8 × Rp22.500 = Rp180.000,00.

 

Soal 7

Indra membeli 1 kuintal beras seharga Rp12.000,00 per kg. Dia lalu menjual beras itu dengan hasil penjualan Rp1.500.000,00. Berapa persentase untung atau rugi yang didapatkan oleh Indra?

Pembahasan:

 

Harga pembelian = (100 × Rp12.000,00) = Rp1.200.000,00

Harga penjualan = Rp1.500.000,00

 

Karena nilai harga penjualan lebih dari harga pembelian, berarti Indra mendapatkan keuntungan.

Keuntungan dari penjualan beras 1 kuintal

= Rp1.500.000,00 – Rp1.200.000,00

= Rp300.000,00.

Persentase keuntungan yang diperoleh Indra bisa dihitung dengan membagi untung dengan harga beli lalu dikalikan 100.

Keuntungan = 300.000/1.200.000 x 100%

= ¼  x 100%

= 25%

Jadi, nilai persentase untungnya adalah 25%.

 

Soal 8

Wati membeli 5 karung beras dengan bruto masing-masing 60 kg dan tara 1%. Berapa rupiah yang harus dibayarkan oleh Wati jika harga beras Rp12.000,00 per kg?

Pembahasan:

Bruto (berat kotor), netto (berat bersih), tara (bruto - netto).

Berat Bruto 5 karung beras: (5 × 60 kg) = 300 kg

Tara 1%: 1/100 × 300 kg = 3 kg

Berat Netto 5 karung beras: 300 kg – 3 kg = 297 kg

Harga beli 5 karung beras (neto),

= 297 × Rp12.000,00

= Rp3.564.000,00

Wati harus membayar Rp3.564.000,00.

 

Soal 9

Pak Deni menerima gaji dari kantornya senilai Rp5.600.000,00 sebulan, dengan penghasilan tidak kena pajak Rp4.800.000,00. Apabila besaran pajak penghasilan (PPh) diketahui 2,5%, berapakah nilai gaji yang diterima Pak Deni per bulan?

Pembahasan:

Besar gaji: Rp5.600.000,00

Penghasilan tidak kena pajak: Rp4.800.000,00

Besar penghasilan kena pajak: Rp5.600.000,00 – Rp4.800.000,00 = Rp600.000,00

Besar pajak penghasilan (PPh)

= 2,5% × penghasilan kena pajak

= 2,5/100 × Rp600.000,00

= Rp15.000,00

 

Gaji bersih yang diterima oleh Pak Deni

= Rp5.600.000,00 – Rp15.000,00

= Rp5.585.000,00

 

Soal 10

Wawan menjual sepatu seharga Rp210.000,00. Dari penjualan itu, ia mendapat untung 5% dari harga beli. Berapakah harga beli sepatu tersebut sebelum dijual Wawan?

Pembahasan:

Harga penjualan bisa dihitung dengan harga pembelian + untung.

Harga penjualan = harga pembelian + 5% harga pembelian

210.000 = 100% harga pembelian + 5% harga pembelian

210.000 = 105% × harga pembelian

Harga pembelian = 100/105 × 210.000

= 200.000

Jadi, harga pembelian sepatu yang dijual Wawan adalah Rp200.000,00.

 

Demikian ulasan mengenai contoh soal aritmatika sosial.

Semoga bermanfaat!