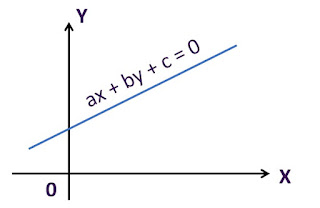20 SOAL CERITA SEHARI-HARI YANG BERKAITAN DENGAN OPERASI HITUNG BILANGAN CACAH (BILANGAN ASLI)

Dalam kesempatan ini akan admin berikan beberapa contoh soal cerita tentang operasi hitung bilangan cacah yang berbentuk pilihan Ganda. Berikut adalah 20 soal cerita harian pilihan ganda tentang operasi bilangan cacah untuk siswa SD/MI.
 
1.     Sarah memiliki 245 stiker, lalu temannya Emma memberinya 389 stiker lagi. Berapa jumlah stiker Sarah sekarang?
A)   524
B)   634
C)   684
D)   774
2.     Sebuah perpustakaan sekolah memiliki 1.732 buku, lalu membeli 865 buku lagi. Berapa total buku yang dimiliki perpustakaan tersebut?
A)   2.497
B)   2.587
C)   2.597
D)   2.697
 
 
3.     Jack memiliki 1.500 kelereng, tetapi ia memberikan 725 kelereng kepada temannya. Berapa kelereng yang tersisa?
A)    775
B)   785
C)   825
D)   875
 
4.     Sebuah toko memiliki 2.450 pulpen dalam stok. Setelah menjual 1.236 pulpen, berapa pulpen yang tersisa?
A)   1.214
B)   1.224
C)   1.234
D)   1.244
 
5.     Seorang petani menanam 124 baris jagung, dengan 36 tanaman jagung di setiap baris. Berapa total tanaman jagung yang ditanam?
A) 3.964
B) 4.064
C) 4.264
D) 4.464
 
6.     Sebuah toko roti membuat 85 roti setiap hari. Berapa jumlah roti yang dibuat dalam 12 hari?
A) 920
B) 1.020
C) 1.120
D) 1.220
 
7.     Seorang guru memiliki 1.200 pensil dan ingin membagikannya secara merata kepada 30 siswa. Berapa pensil yang diterima setiap siswa?
A)   30
B)   35
C)   40
D)   45
 
8.     Sebuah toko buku memiliki 2.750 buku yang disusun merata di 50 rak. Berapa jumlah buku per rak?
A)   45
B)   50
C)   55
D)   60

9.     Lisa membeli 4 bungkus pensil, dengan setiap bungkus berisi 12 pensil. Ia memberikan 15 pensil kepada teman-temannya. Berapa pensil yang tersisa?

A)   28
B)   30
C)   33
D)   36
10.  Sebuah pabrik memproduksi 8.400 mainan dalam 7 hari. Berapa mainan yang diproduksi per hari?
A)   1.100
B)   1.150
C)   1.200
D)   1.250
 

11.  Sebuah sekolah memesan 25 kotak krayon, masing-masing berisi 48 krayon. Jika mereka menerima 1.200 krayon tambahan sebagai donasi, berapa total krayon yang dimiliki?
A)   2.300
B)   2.400
C)   2.500
D)   2.600
 
12.  Ada 64 kursi di aula, lalu ditambahkan 27 kursi lagi. Jika setiap baris memiliki 9 kursi, berapa jumlah total baris kursi?
A)   9
B)   10
C)   11
D)   12
 
13.  Seorang petani memanen 5.250 apel tetapi menjual 3.750 apel. Jika apel yang tersisa dikemas dalam kotak berisi 25 apel, berapa banyak kotak yang dibutuhkan?
A)   50
B)   60
C)   70
D)   80
14.  Sebuah pabrik memproduksi 9.600 masker. Setelah mengirimkan 3.200 masker, sisa masker dikemas dalam karton berisi 400 masker per karton. Berapa jumlah karton yang digunakan?
A)   14
B)   15
C)   16
D)   17
 
15.  Kantin sekolah membuat 125 sandwich setiap hari selama 6 hari. Jika mereka membuat tambahan 230 sandwich pada hari terakhir, berapa total sandwich yang dibuat?
A)   950
B)   1.000
C)   1.050
D)   1.100
 
16.  Sebuah stadion memiliki 75 baris kursi, dengan 80 kursi per baris. Jika mereka menambahkan 600 kursi lagi, berapa total kursi yang tersedia?
A)   5.400
B)   5.600
C)   5.800
D)   6.000
 
17.  Sebuah perusahaan memproduksi 9.000 buku tulis tetapi menjual 6.750 di antaranya. Jika mereka mendonasikan sisa buku secara merata ke 15 sekolah, berapa buku yang diterima setiap sekolah?
A)   130
B)   140
C)   150
D)  160
18.  Seorang peternak mengumpulkan 7.800 telur tetapi menjual 5.200 telur. Jika sisa telur dikemas dalam nampan berisi 30 telur per nampan, berapa jumlah nampan yang digunakan?
A)   75
B)   80
C)   85
D)   90
 
19.  Sebuah taman air memiliki 3.500 pengunjung pada hari Senin, 2.850 pada hari Selasa, dan 4.125 pada hari Rabu. Jika 1.200 pengunjung membeli makanan dan minuman setiap hari, berapa jumlah pengunjung yang tidak membeli makanan atau minuman dalam tiga hari?
A)   6.075
B)   6.175
C)   6.275
D)   6.375
 
20.  Sebuah truk membawa 9.500 kg barang. Truk tersebut mengantarkan 2.750 kg di pemberhentian pertama, 3.150 kg di pemberhentian kedua, lalu membagi sisa muatan secara merata ke 10 toko. Berapa kg barang yang diterima setiap toko?
A)   360
B)   380
C)   400
D)   420
 
Demikianlah sekilas materi tentang soal-soal untuk kelas 6 SD yang dapat digunakan untuk berlatih operasi bilangan cacah dalam kehidupan sehari-hari yang dapat kami sampaikan.
Semoga bermanfaat.

SOAL DAN PEMBAHASAN GRADIEN GARIS LURUS (PERSAMAAN GARIS LURUS)

 Pengertian Gradien

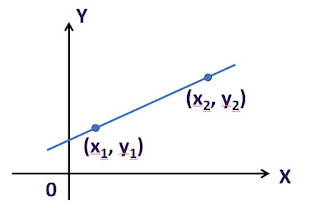
Gradien adalah ukuran kemiringan suatu garis lurus. Dalam matematika, gradien menunjukkan seberapa curam atau landai suatu garis ketika dibandingkan dengan sumbu X. Gradien sering disebut juga sebagai kemiringan garis dan dilambangkan dengan huruf m.

Secara sederhana, gradien menggambarkan perubahan posisi titik pada garis terhadap sumbu X dan sumbu Y. Jika gradien positif, maka garis akan miring ke atas (menanjak) dari kiri ke kanan. Sebaliknya, jika gradien negatif, maka garis akan miring ke bawah (menurun) dari kiri ke kanan. Jika gradien nol, garis akan sejajar dengan sumbu x atau datar.

 

Rumus Mencari Gradien

1. Gradien sebuah garis lurus yang melalui dua titik (x₁, y₁) dan (x₂, y₂)  dapat dihitung dengan rumus berikut:

Dimana:

·           m adalah gradien garis

·           (x₁, y₁) adalah titik pertama pada garis

·           (x₂, y₂) adalah titik kedua pada garis

Dengan menggunakan rumus ini, kita dapat menentukan nilai gradien jika diketahui dua titik pada garis tersebut.

 

2. Garis lurus yang melalui titik (p, 0) dan (0, q), maka gradiennya adalah  m = -q/p.

3. Selain rumus di atas, gradien juga bisa didapatkan dari persamaan garis dalam bentuk y = mx + c, di mana m adalah gradien garis dan c adalah titik potong garis dengan sumbu Y.

4. Garis lurus yang memiliki bentuk ax + by + c = 0 atau ax + by = c, maka gradiennya adalah  m = -a/b.

 

Agar sabahat imath paham, perhatikan beberapa contoh soal berikut.

 

Contoh Soal dan Penyelesaiannya

Contoh 1:

Diketahui dua titik pada sebuah garis, yaitu A(2, 3) dan B(5, 9). Tentukan gradien garis yang melalui kedua titik tersebut.

Contoh 2:

Diketahui persamaan garis y = 5x - 4. Tentukan gradien garis tersebut!

Penyelesaian:

Pada persamaan garis y = mx + c, nilai m adalah gradien.

Dalam persamaan y = 5x - 4, kita bisa melihat bahwa m = 5.

Jadi, gradien garis y = 5x - 4 adalah 5.

 

Contoh 3:

Diketahui persamaan garis 6x - 2y + 7 = 0. Tentukan gradien garis tersebut!

Penyelesaian:

Pada persamaan garis bentuk ax + by + c = 0, maka gradiennya adalah  m = -a/b.

Dalam persamaan 6x - 2y + 7 = 0, kita bisa melihat bahwa nilai a = 6 dan b = -2.

Sehingga gradiennya adalah m = - (-6/2)  = 3

Jadi, gradien garis 6x - 2y + 7 = 0 adalah 3.

 

Contoh 4:

Garis h melalui titik (-3, 0) dan (0, 12). Tentukan gradien garis k tersebut.

Penyelesaian:

Garis lurus yang melalui titik (p, 0) dan (0, q), maka gradiennya adalah  m = -q/p.

Garis h melalui titik (-3, 0) dan (0, 12), berarti dapat ditulis p = -3 dan q = 12.

Gradiennya adalah m = - 12/(-3) = 4

Jadi, garis h melalui titik (-3, 0) dan (0, 12) adalah 4.

 

Demikianlah sekilas materi tentang kesetaraan antarsatuan berat yang dapat kami sampaikan.

Semoga bermanfaat.

Soal-Soal Standar Ujian Sekolah dan Jawabannya Tentang Fungsi dan Komposisi Fungsi

  

Fungsi, komposisi fungsi dan fungsi invers merupakan materi matematika jenjang SMA/MA. Materi Fungsi, komposisi fungsi dan fungsi invers merupakan materi yang sangat penting dipelajari. Materi Fungsi, komposisi fungsi dan fungsi invers ini sering keluar dalam ujian sekolah dan ujian nasional.

Dalam kesempatan ini akan kami berikan beberapa soal latihan matematika khususnya tentang Fungsi, komposisi fungsi dan fungsi invers. Untuk melatih kemampuan kamu dalam menyelesaikan Fungsi, komposisi fungsi dan fungsi invers, berikut beberapa contoh soal Fungsi, komposisi fungsi dan fungsi invers dalam bentuk pilihan ganda beserta dengan kunci jawabannya.

 

1.    Diketahui f(x) = x² – 4x jika f(a + 1) = 5, maka nilai a =  . . . .

A.    a = -2 atau a = 2

B.    a = -2 atau a = 4

C.   a = -1 atau a = 4

D.   a = 1 atau a = -4

E.    a = 2 atau a = -4

Jawaban: B

f(x) = x² – 4x

f(a + 1) = 5

(a + 1)² – 4(a + 1)       = 5

a² + 2a + 1 – 4a – 4    = 5

                 a² – 2a – 3 = 5

                 a² – 2a – 8 = 0

              (a + 2)(a – 4) = 0

               a = -2 atau a = 4

Jadi, nilai a yang memenuhi a = -2 atau a = 4

 

2.    Diketahui fungsi f(x) = x² - 4x - 5 dan g(x) = 4 - 3x. Komposisi fungsi (f o g)(x) = . . . .

       A.   9x² - 12x + 5

       B.   9x² + 12x - 5

       C.   9x² - 12x - 5

       D.   -9x² + 12x - 5

       E.   -9x² - 12x - 5

       Jawaban: C

       f(x) = x² - 4x - 5 dan g(x) = 4 - 3x

       (f o g)(x)  = f(g(x))

                        = f(4 - 3x)

                        = (4 - 3x)² - 4(4 - 3x) - 5

                        = 16 - 24x + 9x² - 16 + 12x - 5

                        = 9x² - 12x - 5

       Jadi, (f o g)(x) = 9x² - 12x - 5.

 

4.    Diketahui komposisi fungsi (f o g)(x) = 4x² + 6x – 5 dan f(x) = 2x + 7. Rumus fungsi g(x) yang bersesuaian dengan komposisi fungsi tersebut adalah ….

       A.   2x² + 6x – 12

       B.   2x² + 3x – 6

       C.   2x² + 3x + 6

       D.   2x² + 3x – 1

       E.    2x² + 3x + 1

       Jawaban: B

 (f o g)(x) = 4x² + 6x – 5 dan f(x) = 2x + 7

           f(g(x)) = 4x² + 6x – 5

      2g(x) + 7 = 4x² + 6x – 5

            2g(x) = 4x² + 6x – 12

              g(x) = 2x² + 3x – 6

Jadi, diperoleh g(x) = 2x² + 3x – 6.

 

5.    Diketahui f(x) = x² – 2x + 6 dan g(x) = x + 3.  Jika fungsi (f o g)(p) = 14, salah satu nilai p positif adalah . . . .

A.     p = 1

B.     p = 2

C.     p = 3

D.     p = 4

E.     p = 6

Jawaban: A

(f o g)(x)    = f(g(x))

                 = f(x + 3)

                 = (x + 3)² – 2(x + 3) + 6

                 = x² + 6x + 9 – 2x – 6 + 6

                 = x² + 4x + 9 

(f o g)(p) = 14

     p² + 4p + 9 = 14

     p² + 4p – 5 = 0

  (p + 5)(p – 1) = 0

  p = -5 atau p = 1

Jadi, nilai p yang memenenuhi adalah p = 1.

 

6.    Diketahui suatu fungsi komposisi (fog)(x) = x² – 9x + 12 dan g(x) = x –  5. Fungsi f(x) adalah . . . .

       A.    f(x)  = x² – x + 8

       B.    f(x)  = x² – x – 8

       C.   f(x)  = x² + x – 8

       D.   f(x)  = x² – 10x – 8

       E.    f(x)  = x² – 10x + 8

       Jawaban: B

(f o g)(x)  = x² – 9x + 12

f(x – 5)  = x² – 9x + 12

Misalkan x – 5 = a, maka  x = a + 5

f(x – 5) = x² – 9x + 12

f(a)  = (a + 5)² – 9(a + 5) + 12

       = a² + 10a + 25 – 9a – 45 + 12

       = a² – a – 8

f(x)  = x² – x – 8

Jadi, fungsi f(x) = x² – x – 8.

  

8.    Diketahui suatu fungsi f(x) = x² – 3x + 6 dan g(x) = x + 4. Grafik Fungsi f(g(x)) memotong sumbu Y di titik . . . .

       A.    (0, –12)

       B.    (0, –10)

       C.   (0, 2)

       D.   (0, 10)

       E.    (0, 12)

       Jawaban: D

f(x) = x² – 3x + 6 dan g(x) = x + 4

f (g(x)) = (x + 4)² – 3(x + 4) + 6

            = x² + 8x + 16 – 3x – 12 + 6

            = x² + 5x + 10

Sehingga y = f(g(x)) dapat ditulis y = x² + 5x + 10.

Grafik fungsi y = x² + 5x + 10 memotong sumbu Y pada saat x = 0.

untuk x = 0 , maka y = 0² + 5(0) + 10  = 10.

Jadi, grafik fungsi y = f(g(x)) memotong sumbu Y dititik (0, 10)

 

 

Demikianlah sekilas materi fungsi dan komposisi fungsi yang kami sampaikan. Semoga bermanfaat.

10 Soal Setara Soal Ujian Sekolah dan Ujian Nasional Matematika SD dan Pembahasan Kesetaraan Antarsatuan Berat

Dalam kesempatan ini akan kami berikan beberapa soal latihan matematika khususnya tentang kesetaraan antarsatuan berat. Untuk melatih kemampuan kamu dalam menghitung berat, berikut beberapa contoh soal satuan berat dalam bentuk pilihan ganda beserta dengan kunci jawabannya.

1.     Berat 1 kg setara dengan …

A.     10 ons

B.     20 ons

C.     50 ons

D.    100 ons

Jawaban: a

 

2.     3 ton + 2 kuintal = … kg

A.     32 kg

B.     230 kg

C.     2.300 kg

D.    3.200 kg

Jawaban: D

 

3.     2,5 kg + 4 hg = ….

A.     254 gram

B.     290 gram

C.     2.540 gram

D.    2.900 gram

Jawaban: D

 

4.     5 ton -  2,6 kuintal = … kg

A.     4.740 kg

B.     4.640  kg

C.     2.400  kg

D.    2.360  kg

 

Jawaban: A

 

5.     2,5 kg + 3 hg - 750 gram = …

A.     1.950 gram

B.     2.050 gram

C.     3.250 gram

D     4.750 gram

Jawaban: B

 

Baca Juga:

KUMPULAN SOAL STANDAR UJIAN SEKOLAH DAN UJIAN NASIONAL KESETARAAN ANTAR SATUAN WAKTU

6.     3,5 gram  – 1,7 dg + 820 mg = ….

A.     2.620 mg

B.     2.720 mg

C.     4.150 mg

D.    4.250 mg

Jawaban: C

 

7.     4,2 ton – 13 kuintal + 630 kg = ….

A.     2.950 kg

B.     3.530 kg

C.     3.700 kg

D.    4.700 kg

Jawaban: B

 

8. Hasil dari 7,4 kg - 52 hg + 310 dag =...

A.     4.500 gram

B.     4.900 gram

C.     5.100 gram

D.    5.300 gram

Kunci jawaban: D

 

9.      12,7 gram - 94 dg + 250 mg =...

A.     578 mg

B.     1.210 mg

C.     3.550 mg

D.    3.650 mg

Kunci jawaban: C

 

10. Hasil dari 2,9 ton + 21,6 kuintal - 2.600 kg =...

A.     2.460 kg

B.     2.640 kg

C.     2.720 kg

D.    3.640 kg

Kunci jawaban: A

 

Demikianlah sekilas materi tentang kesetaraan antarsatuan berat yang dapat kami sampaikan.

Semoga bermanfaat.