Menyelesaikan Persamaan Mutlak
Nilai mutlak suatu bilangan dapat diartikan jarak antara bilangan tersebut dari titik nol(0). Dengan demikian jarak selalu bernilai positif.
Misalnya:
Parhatikan garis bilangan berikut.
Jarak angka 6 dari titik 0 adalah 6
Jarak angka -6 dari titik 0 adalah 6
jarak angka -3 dari titik 0 adalah 3
Jarak angka 3 dari titik0 adalah 3.
Dari penjelesan di atas memang tampak bahwa nilai mutlak suatu bilangan selalu bernilai positif.
Berkaitan dengan menentukan nilai mutlak suatu bilangan, maka muncullah tanda mutlak. Tanda mutlak disimbolkan dengan garis 2 ditepi suatu bilangan atau bentuk aljabar.
Misalnya seperti berikut.
Secara umum, bentuk persamaan nilai mutlak dapat dimaknai seperti berikut.
Jika kita mempunyai persamaan dalam bentuk aljabar, maka dapat dimaknai sebagai berikut.
Jadi, bentuk dasar di atas dpat digunakan untuk membantu menyelesaikan persamaan mutlak.
Lebih jelasnya perhatikan contoh-contoh berikut.
Contoh
Tentukan himpunan penyelesaian dari persamaan nilai Mutlak di bawah ini.
Jawaban:
Bentuk-Bentuk persamaan nilai mutlak di atas dapat diselesaikan sebagai berikut. Pada prinsipnya, langkah langkah penyelesaian nilai mutlak diusahakan bentuk mutlak berada di ruas kiri.
1. Pada bentuk ini ada dua penyelesaian.
(*) x + 5 = 3 , maka x = 3 - 5 = -2
(**) x + 5 = -3, maka x = -3 - 5 = -8
Jadi, himpunan penyelesaiannya adalah {-2, -8}
2. Pada bentuk ini ada dua penyelesaian.
(*) 2x + 3 = 5 , maka 2x = 5 - 3
2x = 2 <==> x = 1
(**) 2x + 3 = -5 , maka 2x = -5 -3
2x = -8 <==> x = -4
Jadi, himpunan penyelesaiannya adalah {-4, 1}
3. Perhatikan bentuk aljabar di dalam tanda mutlak, yaitu x+1. Penyelesaian persamaan nilai mutlak ini juga dibagi menjadi dua bagian.
Bagian pertama untuk batasan x+1>= 0 atau x >= -1
Bagian kedua untuk batasan x+1< 0 atau x < -1
Mari kita selesaikan.
(*) untuk x >=-1
Persamaan mutlak dapat ditulis:
(x + 1) + 2x = 7
3x = 7 - 1
3x = 6
x = 2 (terpenuhi, karena batasan >= -1)
(**) untuk x < -1
Persamaan mutlak dapat ditulis:
-(x + 1) + 2x = 7
-x - 1 + 2x = 7
x = 7 + 1
x = 8 (tidak terpenuhi, karena batasan < -1)
Jadi, Himpunan penyelesaiannya adalah {2}.
4.
Perhatikan bentuk aljabar di dalam tanda mutlak, yaitu 3x + 4. Penyelesaian persamaan nilai mutlak ini juga dibagi menjadi dua bagian.
Bagian pertama untuk batasan 3x+4>= 0 atau x >= -4/3
Bagian kedua untuk batasan 3x+4< 0 atau x < -4/3
Mari kita selesaikan.
(*) untuk x >=-4/3
Persamaan mutlak dapat ditulis:
(3x + 4) = x - 8
3x - x = -8 - 4
2x =-12
x = -6 (tidak terpenuhi, karena batasan >= -4/3)
(**) untuk x < -4/3
Persamaan mutlak dapat ditulis:
-(3x + 4) = x - 8
-3x - 4 = x -8
-3x - x = -8 + 4
-4x = -4
x = 1 (tidak terpenuhi, karena batasan < -4/3)
Jadi, Tidak ada Himpunan penyelesaiannya.
Menyelesaikan Pertidaksamaan Nilai Mutlak
Menyelesaikan pertidaksamaan nilai mutlak caranya hampir sama dengan persamaan nilai mutlak. hanya saja berbeda sedikit pada tanda ketidaksamaannya. Langkah-langkah selanjutnya seperti menyelesaikan pertidaksamaan linear atau kuadrat satu variabel .
Pertidaksamaan mutlak dapat digambarkan sebagai berikut.
Apabila fungsi di dalam nilai mutlak berbentuk ax + b maka pertidaksamaan nilai mutlak dapat diselesaikan seperti berikut.
Lebih jelasnya perhatikan contoh berikut ini.
Contoh
Tentukan himpunan penyelesaian dari Pertidaksamaan nilai mutlak berikut ini.
Jawaban
1. Cara menyelesaikan pertidaksamaan mutlak ini sebagai berikut.
-9 < x+7 < 9
-9 - 7 < x < 9 - 7
-16 < x < 2
Jadi, himpunan penyelesaiannya adalah { x/ -16 < x < 2}
2. Cara menyelesaikan pertidaksamaan mutlak ini dibagi menjadi dua bagian.
(*) 2x - 1 >= 7
2x >= 7 + 1
2x >= 8
x >= 4
(**) 2x - 1 <= -7
2x <= -7 + 1
2x <= -6
x <= -3
Jadi, himpunan penyelesaiannya adalah { x/ x <= -3 atau x >= 4}
3. Kalau dalam bentuk soal ini, langkah menyelesaikan pertidaksamaannya dengan mengkuadratkan kedua ruas.
perhatikan proses berikut ini.
(x + 3)2 <= (2x – 3)2
(x + 3)2 - (2x – 3)2
<= 0
(x + 3 + 2x – 3) - (x + 3 – 2x + 3)
<= 0 (ingat: a2 – b2 =
(a+b)(a-b))
x (6 - x) <=0
Pembuat nol adalah x = 0 dan x = 6
Mari selidiki menggunakan garis
bilangan
Oleh karena batasnya <= 0, maka
penyelesaiannya adalah x <=0 atau x >=6.
Jadi, himpunan penyelesaiannya
adalah {x/ x <= 0 atau x >= 6}.
Mari
selidiki menggunakan garis bilangan
Oleh
karena batasnya <= 0, maka penyelesaiannya adalah x <=0 atau x >=6.
Jadi,
himpunan penyelesaiannya adalah {x/ x <= 0 atau x >= 6}.
4. Menyelesaikan pertidaksamaan nilai mutlak seperti ini lebih mudah menggunakan cara menjabarkan definisi.
Prinsipnya adalah batasan-batasan pada fungsi nilai mutlaknya.
Perhatikan pada 3x + 1 dan 2x + 4.
Dari batasan batasan itu maka dapat diperoleh batasan-batasan nilai penyelesaian seperti pada garis bilangan di bawah ini.
Dengan garis bilangan tersebut maka pengerjaanya dibagi menjadi 3 bagian daerah penyelesaian.
1. Untuk batasan x >= -1/3 ......(1)
(3x + 1) - (2x + 4) < 10
3x + 1 - 2x- 4 < 10
x- 3 < 10
x < 13 .......(2)
Dari (1) dan (2) diperoleh irisan penyelesaian -1/3 <= x < 13Prinsipnya adalah batasan-batasan pada fungsi nilai mutlaknya.
Perhatikan pada 3x + 1 dan 2x + 4.
Dari batasan batasan itu maka dapat diperoleh batasan-batasan nilai penyelesaian seperti pada garis bilangan di bawah ini.
Dengan garis bilangan tersebut maka pengerjaanya dibagi menjadi 3 bagian daerah penyelesaian.
1. Untuk batasan x >= -1/3 ......(1)
(3x + 1) - (2x + 4) < 10
3x + 1 - 2x- 4 < 10
x- 3 < 10
x < 13 .......(2)
2. Untuk batasan -2<= x < -1/3 ......(1)
-(3x + 1) - (2x + 4) < 10
-3x - 1 - 2x - 4 < 10
-5x - 5 < 10
-5x < 15
-x < 3
x > 3 .......(2)
Dari (1) dan (2) tidak diperoleh irisan penyelesaian atau tidak ada penyelesaian.-(3x + 1) - (2x + 4) < 10
-3x - 1 - 2x - 4 < 10
-5x - 5 < 10
-5x < 15
-x < 3
x > 3 .......(2)
3. Untuk batasan x < -2 ......(1)
-(3x + 1) + (2x + 4) < 10
-3x - 1 + 2x + 4 < 10
-x + 3 < 10
-x < 7
x > -7 .......(2)
Dari (1) dan (2) diperoleh irisan penyelesaian -7 < x < -2.
-(3x + 1) + (2x + 4) < 10
-3x - 1 + 2x + 4 < 10
-x + 3 < 10
-x < 7
x > -7 .......(2)
Jadi, himpunan penyelesaiannya adalah {x/ -1/3 <= x < 13 atau -7 < x < -2}.
Perhatikan contoh Pertidaksamaan mutlak lainnya berikut.
VIDEO TUTORIAL Cara Menyelesaikan Persamaan Nilai Mutlak #1
VIDEO TUTORIAL Cara Menyelesaikan Persamaan Nilai Mutlak #2
VIDEO TUTORIAL Cara Menyelesaikan Pertidaksamaan Nilai Mutlak #1
VIDEO TUTORIAL Cara Menyelesaikan Pertidaksamaan Nilai Mutlak #2
[VIDEO TUTORIAL] Cara Mudah Menyelesaikan Persamaan Mutlak Satu Variabel yang Memuat Dua Tanda Mutlak
[VIDEO TUTORIAL] Cara Mudah Menyelesaikan Persamaan Mutlak Satu Variabel yang Memuat Tiga Tanda Mutlak
[VIDEO TUTORIAL] Cara Mudah Menyelesaikan Pertidaksamaan Mutlak Satu Variabel yang Memuat Dua Tanda Mutlak
[VIDEO TUTORIAL] Cara Mudah Menyelesaikan Pertidaksamaan Mutlak Satu Variabel yang Memuat Tiga Tanda Mutlak
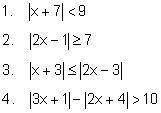
mau tanya ..
BalasHapuskalo |x² + x - 1 | ≤ 1
cara jawabnya gmana ya ?
|x² + x - 1 | ≤ 1
Hapus-1 < x² + x - 1 < 1
0 < x² + x < 2
0 < x(x+1) < 2
penyelesaian:
0 < x(x+1) dan x(x+1)<2
Jawaban itu selalu dalam bentuk himpunan x saja. Tidak dalam bentuk x^2.
HapusJawabannya kurang tepat
Jawaban itu selalu dalam bentuk himpunan x saja. Tidak dalam bentuk x^2.
HapusJawabannya kurang tepat
mau tanya yg pertidaksamaan no 1, kenapa angka 9 nya bisa jadi ada dua ?
Hapusterima kasih
Solusi nya memang seperti itu, supaya dipermudah aja( langsung dirangkap jadi satu yang seharusnya ada dua cara)
HapusKalau |2x-1| = |4x-3| berapa
BalasHapusHP = {1}
Hapus1/2 DAN 1 TO MAS
HapusX1=-1 dan X2=2/3
Hapus{X|X=1 atau X=2/3}
Hapusmau tanya F(x)2x+4
BalasHapussama F(x)5-2x
butuh Bantuannya
Kalo |2x-6|+|x-1| pake cara yg mana? Yg 4 bukan?
BalasHapusKalo |2x-6|+|x-1| pake cara yg mana? Yg 4 bukan?
BalasHapusmaaf ingin mencoba membantu.. itu persamaan atau pertidaksamaan?
HapusItu dselesaikan dengan menggunakan definisi..
Hapuskalau pakai definisi berarti ada tiga syarat
HapusKomentar ini telah dihapus oleh pengarang.
BalasHapus|3x-3|=|3x+5| Itu berapa?
BalasHapusHP= {-1/3}
HapusDgn menggunakan defenisi :
HapusJika
|a| = |b|
Maka
a = b
a = -b
Jadi utk soal itu..
(i)
3x-3 = 3x+5
-3 = 5
Bukan penyeleseain krn x nya telah habis
(ii)
3x-3 = -(3x+5)
3x-3 = -3x-5
6x = -2
x = -1/3
Hp = {-1/3}
X1 = 0 dan X2 = -1/3
Hapus-5|3x-7|+4=14
HapusKalo seumpama 3x²-x-2>0 gimana pengerjaanya
HapusMemakai cara (-b±√(b²-4.a.c))/2a
Hapus(1±√(1-4.3.-2)/6
(1±√(1+24)/6
(1±√25)/6
Maka hasilnya bisa dua, yakni:
(1+5)/6=6/6=1
(1-5)/6=-4/6=-2/3
Jadi, x-nya bisa jadi 1 atau -2/3, harus pengujian terlebih dahulu.
|y|<3 caranya gimana ?
BalasHapus|y|<3
Hapusy<-3 atau y<3
yang benar y>-3 atau y<3
Hapus|-3x + 1/2 |, x bilangan R
BalasHapusItu cara nya gimana?
kalo |x+1|=2x-3 caranya gimana ya?
BalasHapus|x+1|=2x-3
Hapusx+1=2x-3 atau x+1=-(2x-3)
x-2x=-3-1 x+1=-2x+3
-x =-4 x+2x=3-1
x = 4 3x=2
x=2/3
Jadi Hp={4>x>2/3}
X^2+2x+1=4x^2-12x+9
Hapus-3x^2+14x-8=0
(-3x+2)(x-4)=0
Hp = {2/3,4}
apa definisi persamaan nilai mutlak satu variabel?
BalasHapusMau tanya jawaban
BalasHapus-5|3×-7|+4=14
X1 = 5/3 dan X2 = 3
HapusMau tanya jawaban
BalasHapus-5|3×-7|+4=14
-5|3×-7|+4=14
Hapus-5|3×-7|=10
|3×-7|=-2
HP{}
karena nilai mutlak tidak mungkin bernilai negatif
Kalo hsil dri ini brp??
BalasHapus|2×4-10|+|1-2×3|×|1+2|
Kalau |x-2| / |x+3| = 4
BalasHapusGimana carany ya?
Terimakasih ilmu nyaa pak :)
BalasHapusKomentar ini telah dihapus oleh pengarang.
BalasHapusBisa minta tlg cara mencari HP dari |x|+|x-5|=5
BalasHapusKomentar ini telah dihapus oleh pengarang.
BalasHapusHP={0, 2/3}
HapusHP = {0,2/3}
HapusKomentar ini telah dihapus oleh pengarang.
BalasHapuskalau |3x-1|<8 gimana caranya?
BalasHapuspake konsep nilai mutlak:
Hapus1. 3x-1<8
3x<9
x<3
2. -3x+1<8
-3x<7
x> -7/3
Jadi HP {3,-7/3}
|3x-1|<8 -(8 )
Hapus-(-8)
|3x-1|<8
3x-1<8
3x<8+1
3x<9
x<3
|3x-1|<-8
3x-1<-8
3x<-8+1
3x<-7
x<-7/3
jadi HP={3,-7/3}
|3x-1|<8
Hapus-8<3x-1<8
-8+1<3x<8+1
-7<3x<9
-7/3<x<9/3
-7/3<x<3
mau tanya kl nilai mutlak dari|2x-1/4x tambah 3|
BalasHapusKalo |5/x-1|= 1/2 gimana ya?
BalasHapusKalo |5/x-1|= 1/2 gimana ya?
BalasHapusKalo |4-3x|=|-4| gimana ?
BalasHapusKalo |4-3x|=|-4| gimana ?
BalasHapusKalo 3|x+2|-5>|x+2|+7
BalasHapusHP = x>-4
HapusKak mau nanya klo soalnya kayak gini,,, x/2 2<5 caranya gimana
BalasHapusKak mau nanya klo soalnya kayak gini,,, x/2 2<9 caranya gimana
BalasHapusKalo |-3b +2 |> 8 itu gimana ya caranya?
BalasHapusMau minta tolong jugaa HP dari
BalasHapus|x|²-3|x|-4= 0
|x-1||2x+1|=2
BalasHapusItu gimna ya??
|x-1||2x+1|=2
BalasHapusItu gimna ya??
HP= x=-1
Hapus|x-1||2x+1|=2
BalasHapusItu gimna ya??
Kalo |2√3-3| itu nilai mutlaknya gmn?
BalasHapus|X(kuadrat)-3|<=1 mohon bntuannya
BalasHapus|X(kuadrat)-3|<=1 mohon bntuannya
BalasHapus|2x+4|<|x-5|
BalasHapusBantu dong!!
|2x+4|<|x-5|
BalasHapusBantu dong!!
|2x+4|<|x-5|
BalasHapusBantu dong!!
|x+2| < |x+3| itu berapa pak?
BalasHapus|3x+8|
BalasHapus—————— =1
|2x-3|
Berapa ya ?
Kalau |x-3|=|x+2| gimana ya caranya
BalasHapus2 | x -1| > | x + 3|
BalasHapus-carilah nilai x ?
-tentukan hpp dari data tersebut.
kalau |x-1|=|3x+2| berapa Himpunansolusinya? terimakasih;)
BalasHapuskalau |x-1|=|3x+2| berapa Himpunansolusinya? terimakasih;)
BalasHapus|x²-10x-14| = 10
BalasHapusMinta tolong ya
Cara penyelesaiannya gimana yaa ?
Sebelumnya Makasih
Kalo penyelesaiannya ini gimana cara nya
BalasHapus|2 x 4 - 10| + |1 - 2 x 3| x |1+2|=
|5×-6|-4=10
BalasHapus|5×-6|-4=10
BalasHapus|5×-6|-4=10
BalasHapus|5×-6|-4=10
BalasHapuskalo |15y-6|=|7y+18|, cara nyari "y" nya gmana?
BalasHapusKalo pertidaksamaan ini gimana?
BalasHapus|x²-3x+1|<1=....
|x+2|>|x+1|=....
3|x-1|>1=....
|3-2x|<5=.....
Saya mau nanya kalo, menyelesaikan setiap permasalahan nilai mutlak berikut, itu caranya gmna?tolong bantuannya
HapusBagian 1
|4-3x|=|-4|
Bagian 2
a).|2x+5|=|7-2y|
b).|4x-3|=-|2x-1|
kalo |5-3x| > |x-5| gimanaya? sekalian caranya ya.. makasih..
BalasHapusKalau |5-|2-x|-1|=3 caranya gimana ya?
BalasHapuskalo |x+2|^2 + 2|x+2| - 15 》0 bagaimana ya besok saya ulangan
BalasHapus|X-2|>-3x gimana caranya?
BalasHapusNomor 4 soalnya lebih dari ko jawabnya kurang dari
BalasHapusNomor 4 soalnya lebih dari ko jawabnya kurang dari
BalasHapusKak mau nanya dong,
BalasHapusIni cara kerjanya gimana yah?
|4x-3| = -|2x-1|
1. |x+4|+|5-2x|-|x-2| untuk x>10?
BalasHapus2.|3x-6|-|x-4| |x+2| untuk 2<x<4
Terima kasih pak. Pas banget lagi ngajarin adek kls X
BalasHapusjaki y={3x-2}-1,untuk -2<= x<=5 dan x bilangan real??
BalasHapus{}=harga mutlak
jaki y={3x-2}-1,untuk -2<= x<=5 dan x bilangan real??
BalasHapus{}=harga mutlak
Kalau |3x-9|=|1-2x|+1
BalasHapusJawabannya berapa kak?
Kalau |3x-9|=|1-2x|+1
BalasHapusJawabannya berapa kak?
cra menentukan nilai mutlak ini gmn?
BalasHapus{2x+3} untuk nilai x bilangan real
{-2x+5} untuk nilai x bilangan real
{12}-{-3}
{-24/36}x{-6}
tolong diberi penjelasan mengenai contoh soal pertidaksamaan nomor 4 di atas, mengenai penentuan batasnya, dan nilai mutlak yg dipilih di atasnya. terima kasih sebelumnya. jazakumullahu khairan
BalasHapuskalo cara menentukan soal ptnm yg seperti ini gimana??
BalasHapus1.|2x+1|<|2x-3|
2.|x+3/x-4|< 2
tolong bantuannya...
kalo cara menentukan soal ptnm yg seperti ini gimana??
BalasHapus1.|2x+1|<|2x-3|
2.|x+3/x-4|< 2
tolong bantuannya...
Mau Tanya kalo soal yg seperti ini gimana mengerjakannya? |x+3|=>|x-4| tolong bantuannya...
BalasHapusmau tanya min, contoh soal pertidaksamaan nilai mutlak yg no. 4 itu penjelasan untuk pemilihan nilai mutlak yg sesuai untuk batas di persekitaran -2 dan -1/3 itu bagaimana?
BalasHapusterima kasih sebelumnya. blog ini sangat mudah membantu.
Mau tanya,kalau [2x+2] >= 4x -1 apa boleh yang di jadiin negativ dan positif yang [2x+2] Atau harus a nya yaitu 4x -1?
BalasHapusHarus yang 4x - 1
HapusJawabannya apa ya ? |x+5|<|1-9x|
BalasHapusmau tanya 3<=x+2<=8 berapaa?
BalasHapuskalo |3x-6| > |3x+1| gimana caranya?
BalasHapuskalo (2x-5)kuadrat -3(2x-5)>10
BalasHapuskalo ini gimana caranya?
BalasHapus|x-1|-|x+2|<=2
kalau yg ini bgmn caranya?
BalasHapus|x+2|>2|2x-1|
Kalau
BalasHapusNo. 1: |X-5| / |2x| = -4 tidak sama dengan nol
No. 2: 5 |2x-3| = 2 |3-5x|
Kalau soal yang gini gimana caranya |9-2x|=|4x|
BalasHapusKalau soal yang gini gimana caranya |9-2x|=|4x|
BalasHapusmaaf, mau tanya . kalau 2x-5/x-3 (kurang dari atau sama dengan) 1 = ....
BalasHapusMinta tolong diposting bagaimana kalau ada nilai mutlak di dalam nilai mutlak
BalasHapusmisalkan pada masalah ||x|+3x|<2
kalo penyelesaian ini apa ya 7|x+1|+2x =7
BalasHapusKalau soal nya gini bentuk sederhana dari |x+4|+|5-2x|-|x-2| jika nilai x>10
BalasHapus
BalasHapusmohon bantuannya :)
1. Tentukan nilai-nilai x dari pertidaksamaan dibawah inia:
a. x²-3x+1<1
b. |x+2|>|x+1|
c. 3|x-1|>1
d. |3-2x|<5
2. Tentukan nilai-nilai x pada persamaan berikut :
a. -9 < x+7 < 9
b. 2x-1<7
mohon bantuannya:
BalasHapus1. Tentukan nilai-nilai x dari pertidaksamaan dibawah inia:
a. x²-3x+1<1
b. |x+2|>|x+1|
c. 3|x-1|>1
d. |3-2x|<5
2. Tentukan nilai-nilai x pada persamaan berikut :
a. -9 < x+7 < 9
b. 2x-<7
kalo |-4|+|5|-|-3|=
BalasHapus|x-1|=7 maka nilai x + 2 =
BalasHapusx-1=7
Hapusx = 8 (memenuhu)
x-1=-7
x = -6 (tdk memenuhi)
x+2 = 8+2 = 10
Makasi ya
BalasHapusMakasi ya
BalasHapusMakasi ya
BalasHapusKalo |2-x|≥3|x-1|
BalasHapusBagaimana kalo ini mas
BalasHapus|6-2x|≥ 7
6-2x≥ 7
Hapus-2x≥1
x<= -1/2
6-2x≥-7
-2x≥-13
x≥13/2
hp ={-1/2, 13/2}
*<= artinya: kurang dari sama dengan
Maaf kalo begini gimana? |2x+3|+|x -1|=2 Terimakasih
BalasHapusBagaimana kalo 3<|x-2|<7
BalasHapus3<|x-2|<7
Hapus3+2<x<7+2
5<x<9
Kalo |x+2|>3|x-4|
BalasHapusPertidaksamaan Mutlak
Mau tanya
BalasHapusKalo |-x-16/x+5|<3
Terima kasih
gimana kalau ini kak |x-2|>3 ??
BalasHapusmau tanya kalau soal seperti ini |x| <= 3x-2 itu cara penyelesaiannya gimana ya ?
BalasHapusMau tanya ..
BalasHapus|2x-2|+|3x-8|=5
Cara ngerjainnya gimana ya?
kalau ini gimana ya |3/x-2|<4 dan ini x(x-2)(x+3)> 0 tolong dong...
BalasHapusSederhana dari |6x-12|-|x-8||x+2| untuk nilai x>5
BalasHapusMau nanya kalok|x-2|<|2X+1|
BalasHapusmau nanyak kalo gni gmna pnyelesaiannya |6x|-|24-4|kurang dari sama dengan 3 gmna ya ?
BalasHapus|3-x|≤ |2x-1|
BalasHapusitu kenapa yang di soal nomer dua saat di penyelesaian kedua 5 nya jadi negatif ?
BalasHapus(**) 2x + 3 = -5 , maka 2x = -5 -3
2x = -8 <==> x = -4
bukannya seharusnya 2x + 3 = 5 ??????????????
Komentar ini telah dihapus oleh pengarang.
BalasHapusmau tanya nich
BalasHapus|x-1| + |x-4|= 6
nich jawab nya g mna ya
mohon bantuan nya
cari sendiri belajar sakit :v
Hapusbelajar aja kalo mau tau
Hapuswaloh
BalasHapusiya kah waloh
Hapusjiah
BalasHapusjiah jua
Hapusbuaaaahahaahahaha sependapat gw ama raden :v
Hapusتاي
BalasHapuskai gaul kh kai legend :v
BalasHapusanjing lu pada
BalasHapusraden tu subhan :v
BalasHapussubhan pacul helm bogo ganti helm plywood
BalasHapushitung nilai x .
BalasHapus| 3 + 7/x | > 1 ...........
tolong info jwbn
(X²+2)-5(X²+2)>6
BalasHapushitung nilai x ??
X²-2x-3 / x-1 >0
BalasHapusKomentar ini telah dihapus oleh pengarang.
BalasHapusx2-|x-1|=0 ,apa jawabannya mohon dibantu
BalasHapus|x²+x-20| <= x²+x-20
BalasHapusHimpunan penyelesainnya gimana?
2|x-1|^2-3|x-1|+1<0
BalasHapusHimpunan penyelesaiannya gimana kk?
Permisi saya mau tanya himpunan penyelesaian ketaksamaan -3<1-6x≤4= ini gimana ya kak?
BalasHapusSederhana kan |3+x|-|2x+6| untuk x>-3
BalasHapuskalo |12-6x|<24 itu berapa
BalasHapusmau tanya kalo 1/4(1/5(2/3=1/2)-2/5)
BalasHapusmau nanya kalau [2x-3]<[x+2] berapa ya himpunan penyelesaiannya?
BalasHapusMaaf mau tanya kalau harga mutlak (2+7/2)<2 berapa penyelesaiannya?
BalasHapusklo ini gimana |x-2|<2|x-2|-3
BalasHapusAda 3 orang berbelanja dari tokoh
BalasHapusAndi membeli 3 unit barang A dan 4 unit barang B dan 1 unit barang C dengan harga Rp83.000 . Budi membeli 6 unit barang A,2 unit barang B dan 1 unit barang C. Dengan harga Rp.86.000 dan chandra membeli 2 unit barang A,5 barang B dan 10 unit barang C dengan harga Rp.158.000 tentukan!!!
a. Berapa harga barang per unit barang A,B,C.
b.jika delton membeli 6 unit barang A,3 unit barang B dan 9 unit barang C berapa harganya?
Ada 3 orang berbelanja dari tokoh
BalasHapusAndi membeli 3 unit barang A dan 4 unit barang B dan 1 unit barang C dengan harga Rp83.000 . Budi membeli 6 unit barang A,2 unit barang B dan 1 unit barang C. Dengan harga Rp.86.000 dan chandra membeli 2 unit barang A,5 barang B dan 10 unit barang C dengan harga Rp.158.000 tentukan!!!
a. Berapa harga barang per unit barang A,B,C.
b.jika delton membeli 6 unit barang A,3 unit barang B dan 9 unit barang C berapa harganya?
Ada 3 orang berbelanja dari tokoh
BalasHapusAndi membeli 3 unit barang A dan 4 unit barang B dan 1 unit barang C dengan harga Rp83.000 . Budi membeli 6 unit barang A,2 unit barang B dan 1 unit barang C. Dengan harga Rp.86.000 dan chandra membeli 2 unit barang A,5 barang B dan 10 unit barang C dengan harga Rp.158.000 tentukan!!!
a. Berapa harga barang per unit barang A,B,C.
b.jika delton membeli 6 unit barang A,3 unit barang B dan 9 unit barang C berapa harganya?
Ada 3 orang berbelanja dari tokoh
BalasHapusAndi membeli 3 unit barang A dan 4 unit barang B dan 1 unit barang C dengan harga Rp83.000 . Budi membeli 6 unit barang A,2 unit barang B dan 1 unit barang C. Dengan harga Rp.86.000 dan chandra membeli 2 unit barang A,5 barang B dan 10 unit barang C dengan harga Rp.158.000 tentukan!!!
a. Berapa harga barang per unit barang A,B,C.
b.jika delton membeli 6 unit barang A,3 unit barang B dan 9 unit barang C berapa harganya?
Yang tau bantu dong ..(12-12/x)>3
BalasHapusitu soal no 4 kok tanda lebih besar(>) bisa berubah jd lebih kcil(<)??
BalasHapusSelesaikan persamaan berikut
BalasHapus|2x-1| = x²-1
Bagaimana cara penyelesaiannya?
|3x-1|=2
BalasHapusBerapa mas
3x-1=2
Hapus3x=2+1
3x=3
x=1
-(3x-1)=2
-3x+1=2
-3x=2-1
-3x=1
-x=1/3
x=-1/3
Hp={-1/3,1}
2x-3/x+1 > 0
BalasHapusberapa ka?
saya ingin bertanya di nomor 4 contoh soal pertidaksamaan kan itu tandanya > , kenapa di pembahasnnya jadi < ya ?
BalasHapusMau nanya
BalasHapus|5x -3| = |1-3x|
Bagaimana cara penyelesaiannya
Komentar ini telah dihapus oleh pengarang.
BalasHapus2x-3≤x-5<3x+9 cara mencari hp nya gmna yah? Minta tolong d jelasin ka.terimakasih
BalasHapus|1/x-3|>6 berapa ???
BalasHapusKomentar ini telah dihapus oleh pengarang.
BalasHapusno.1
Hapus2x + y =12
x - y =3
tentukan nilai x dan y
no.2
x - 2y + 2 =6
3x +y - 2z =4
7x - 6y - z =10
tentukan nilai x y dan z
Mau nanya
BalasHapus|x|≤-1
Itu gimana ya?
Mau tanya nih kalau misal
BalasHapus|x|+|x-5|=5
itu gimana cara menyelesaikannya?
Mau tanya kalau
BalasHapus(2X-10), XE bilagan bulat??? Gimana
Terimo kasih
|x|<|x-3|
BalasHapusItu gimana
|x|<|x-3|
BalasHapusItu gimana
soal no 2, antara soal sama jawaban kok beda sih? -_-
BalasHapusTerima kasih, postingannya lumayan membantu ^^
BalasHapuska mau nanya, 6<x²+5x <6 brp y ka jadiny?
BalasHapusKalo gini gimana kak x-6≤|3-2x|
BalasHapusCara tentukan nilai x dari |1/x+3|>6 gimana yah min😊
BalasHapus