IMATH: PERBANDINGAN TRIGONOMETRI

15 November

PERBANDINGAN TRIGONOMETRI

Trigonometri

Trigonometri adalah cabang matematika yang membahas hubungan antara perbandingan sisi-sisi segitiga siku-siku dengan sudut-sudutnya. Perbandingan yang digunakan untuk mempelajari hubungan ini disebut perbandingan trigonometri, yaitu sinus, kosinus, tangen, kotangen, sekan, kosekan. Kata trigonometri merupakan turunan Latin abad ke-16 dan konsepnya diberikan oleh matematikawan Yunani bernama Hipparchus.

Dalam artikel di bawah ini, kita akan memahami dasar-dasar trigonometri, berbagai identitas-rumus trigonometri, dan contoh atau aplikasi trigonometri dalam kehidupan nyata.

Pengantar Trigonometri

Trigonometri adalah salah satu cabang terpenting dalam Matematika. Kata trigonometri dibentuk dengan menggabungkan kata 'Trigonon' dan 'Metron' yang masing-masing berarti segitiga dan ukuran. Ini adalah studi tentang hubungan antara sisi-sisi dan sudut-sudut pada segitiga siku-siku. Dengan demikian, hal ini membantu dalam menemukan ukuran sisi yang tidak diketahui dari segitiga siku-siku menggunakan rumus dan identitas berdasarkan hubungan ini.

Dasar-Dasar Trigonometri

Dasar-dasar trigonometri berurusan dengan pengukuran sudut dan masalah yang terkait dengan sudut. Ada tiga fungsi dasar dalam trigonometri: sinus, kosinus, dan tangen. Ketiga perbandingan atau fungsi dasar ini dapat digunakan untuk memperoleh fungsi trigonometri penting lainnya: kotangen, sekan, dan kosekan. Semua konsep penting yang tercakup dalam trigonometri didasarkan pada fungsi-fungsi ini. Oleh karena itu, selanjutnya, kita perlu mempelajari fungsi-fungsi ini dan rumus masing-masing terlebih dahulu untuk memahami trigonometri.

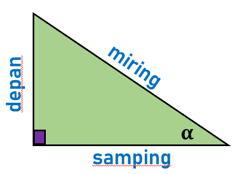
Segitiga Siku-siku

Dalam segitiga siku-siku, kita memiliki tiga sisi berikut.

Sisi Depan adalah sisi yang berada di depan sudut θ.

Sisi Samping adalah sisi yang berdekatan dengan sudut θ.

Sisi Miring adalah sisi yang di depan sudut siku-siku.

Perbandingan Trigonometri

Ada enam perbandingan dasar dalam trigonometri yang membantu dalam menetapkan hubungan antara perbandingan sisi-sisi segitiga siku-siku dengan sudutnya. Jika θ adalah sudut dalam segitiga siku-siku, yang terbentuk antara alas dan sisi miring, maka:

Nilai dari tiga trigonometri lainnya: cot, sec, dan cosec. Nilai tersebut bergantung pada tan, cos, dan sin. Masing-masing nilai tersebut diberikan di bawah ini.