IMATH: BARISAN DAN DERET ARITMETIKA

Barisan Aritmatika

Barisan aritmatika adalah barisan yang selisihnya (beda) tetap konstan antara dua suku yang berurutan. Mari kita ingat kembali apa yang dimaksud barisan. Barisan adalah kumpulan angka yang mengikuti suatu pola. Misalnya, barisan 1, 6, 11, 16, … adalah barisan aritmatika karena ada pola di mana setiap angka diperoleh dengan menambahkan 5 pada suku sebelumnya. Kita memiliki dua rumus barisan aritmatika, yaitu:

*Rumus untuk mencari suku ke-n dari barisan aritmatika

*Rumus untuk mencari jumlah n suku pertama dari barisan aritmatika

Jika kita ingin mencari suku apa pun dalam barisan aritmatika, maka kita dapat menggunakan rumus barisan aritmatika. Mari kita pelajari definisi barisan aritmatika dan rumus barisan aritmatika beserta turunannya dan disertai contoh yang banyak untuk pemahaman yang lebih baik.

Apa itu Barisan Aritmatika?

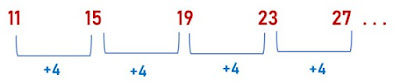
Baris aritmatika didefinisikan dalam dua cara. Yang pertama adalah "deretan di mana selisih antara setiap dua suku yang berurutan adalah sama" . Yang kedua dalam deret aritmatika, "setiap suku diperoleh dengan menambahkan bilangan tetap (positif atau negatif atau nol) ke suku sebelumnya". Berikut ini adalah deret aritmatika karena setiap suku diperoleh dengan menambahkan bilangan tetap 4 ke suku sebelumnya.

Contoh Deret Aritmatika

Perhatikan deret 3, 6, 9, 12, 15, .... adalah deret aritmatika karena setiap suku diperoleh dengan menambahkan bilangan konstan (3) ke suku sebelumnya.

Dengan demikian diperoleh

Suku pertama, a = 3

Selisih (beda), b = 6 - 3 = 9 - 6 = 12 - 9 = 15 - 12 = ... = 3

Jadi, deret aritmatika dapat ditulis sebagai a, a + b, a + 2b, a + 3b, ....

Mari kita bentuk pola ini untuk contoh di atas.

a, a + b, a + 2b, a + 3b, a + 4b , ...

= 3, 3 + 3, 3 + 2(3), 3 + 3(3), 3 + 4(3),...

= 3, 6, 9, 12,15,....

Beberapa contoh deret aritmatika lainnya adalah:

5, 8, 11, 14, ...

80, 75, 70, 65, 60, ...

2, 7, 12, 17, 22, 27, ...

Rumus Deret Aritmatika

Suku pertama deret aritmatika adalah a, beda persekutuannya adalah b, n adalah banyaknya suku. Bentuk umum barisan aritmetika adalah a, a + b, a + 2b, a + 3b,......hingga n suku. Kita memiliki berbagai rumus yang terkait dengan deret aritmatika yang digunakan untuk menghitung suku ke-n, jumlah n suku deret aritmatika, atau beda persekutuan deret aritmatika tertentu.

Rumus pada barisan dan deret aritmatika diberikan sebagai berikut,

Suku ke-n :U_n = a + (n - 1)b

Jumlah n suku pertama : S_n = (n/2) [2a + (n - 1)b]

Beda (selisih) : b = a_n - a_n-1

Suku ke-N Deret Aritmatika

Suku ke-n deret aritmatika U₁, U₂, U₃, ... diberikan oleh U_n = U₁ + (n - 1)b. Ini juga dikenal sebagai suku umum deret aritmatika. Ini secara langsung mengikuti pemahaman bahwa deret aritmatika U₁, U₂, U₃, ... = U₁, U₁ + b, U₁ + 2b, U₁ + 3b,... Tabel berikut menunjukkan beberapa deret aritmatika beserta suku pertama, beda umum, dan suku ke-n.

5, 8, 11, 14, ... mempunyai suku pertama (a) = 5 dan beda (b) = 3

80, 75, 70, 65, 60, ... mempunyai suku pertama (a) = 80 dan beda (b) = -5

2, 7, 12, 17, 22, 27, ... mempunyai suku pertama (a) = 2 dan beda (b) = 5

Rumus Rekursif Deret Aritmatika

Rumus di atas untuk mencari suku ke-n dari deret aritmatika digunakan untuk mencari suku apa pun dari deret tersebut ketika nilai 'U₁' dan 'b' diketahui. Ada rumus lain untuk mencari suku ke-n yang disebut "rumus rekursif deret aritmatika" dan digunakan untuk mencari suku (U_n) dari deret tersebut ketika suku sebelumnya (U_n-1) dan 'b' diketahui.

Rumus tersebut adalah:

U_n = U_n-1 + d

Rumus ini mengikuti definisi deret aritmatika.

Contoh:

Carilah U₂₁ dari deret aritmatika jika U₁₉ = -72 dan b = 7.

Solusi:

Dengan menggunakan rumus rekursif,

U₂₀ = U₁₉ + d = -72 + 7 = -65

U₂₁ = U₂₀ + d = -65 + 7 = -58

Jadi, diperoleh U₂₁ = -58.

Deret Aritmatika

Penjumlahan rumus deret aritmatika digunakan untuk mencari jumlah n suku pertamanya. Perhatikan bahwa jumlah suku deret aritmatika dikenal sebagai deret aritmatika. Perhatikan deret aritmatika yang suku pertamanya adalah U₁ (atau a) dan bedanya adalah b. Jumlah n suku pertamanya dilambangkan dengan S_n. Maka

Jika suku ke-n tidak diketahui: S_n= n/2 [2a + (n - 1) b]

Jika suku ke-n diketahui: S_n = n/2 [a + U_n]

Contoh

Ibu Natalie memperoleh penghasilan $200.000 per tahun dan gajinya meningkat sebesar $25.000 per tahun. Maka, berapa total penghasilannya pada akhir 5 tahun pertama?

Solusi:

Jumlah penghasilan Ibu Natalie untuk tahun pertama adalah, a = 2.00.000. Kenaikan per tahun adalah, b = 25.000. Kita harus menghitung penghasilannya dalam 5 tahun pertama. Jadi n = 5. Substitusikan nilai-nilai ini ke dalam rumus jumlah deret aritmatika,

S_n= n/2 [2a + (n - 1)b]

⇒ S_n = 5/2(2(200.000) + (5 - 1)(25.000))

= 5/2 (400.000 +100.000)

= 5/2 (500.000)

= 1.250.000

Ia memperoleh penghasilan $1.250.000 dalam 5 tahun. Kita dapat menggunakan rumus ini agar lebih membantu untuk nilai 'n' yang lebih besar.

Jumlah Deret Aritmatika

Mari kita ambil deret aritmatika yang suku pertamanya adalah U₁ dan bedanya adalah b. Maka jumlah suku pertama 'n' dari barisan tersebut diberikan oleh

S_n = U₁ + (U₁ + b) + (U₁ + 2b) + … + U_n ... (1)

Mari kita tulis jumlah yang sama dari kanan ke kiri (yaitu, dari suku ke-n ke suku pertama).

S_n = U_n + (U_n – B) + (U_n – 2B) + … + U₁ ... (2)

Dengan menambahkan (1) dan (2), semua suku dengan 'd' akan dibatalkan.

2S_n = (U₁ + U_n) + (U₁ + U_n) + (U₁ + U_n) + … + (U₁ + U_n)

Sebanyak n suku

2S_n = n (U₁ + U_n)

S_n = (n/2) [U₁ + U_n]

Dengan mensubstitusikan U_n = U₁ + (n – 1) b ke dalam rumus terakhir, kita memperoleh

S_n = n/2 [U₁ + U₁ + (n – 1)b] atau

S_n = n/2 [2U₁ + (n – 1)b]

S_n = n/2 [2a + (n – 1)b]