Diskriminan Persamaan Kuadrat
Diskriminan banyak digunakan dalam permasalahan
persamaan kuadrat dan digunakan untuk menemukan sifat akar. Meskipun menemukan
diskriminan untuk polinomial apa pun tidaklah mudah, ada rumus untuk menemukan diskriminan
persamaan kuadrat dan persamaan kubik yang memudahkan pekerjaan kita.
Mari kita pelajari lebih lanjut tentang diskriminan
beserta rumusnya dan mari kita pahami juga hubungan antara diskriminan dan
sifat-sifat akar.
Apa itu Diskriminan dalam
Matematika?
Diskriminan polinomial dalam matematika adalah fungsi
dari koefisien polinomial. Diskriminan berguna dalam menentukan jenis solusi
persamaan polinomial tanpa benar-benar menemukannya. Yaitu, diskriminan untuk mendiskriminasi
solusi persamaan kuadrat atau polinomial (misalnya: sama dan tidak sama; nyata
dan tidak nyata) dan karenanya disebut "diskriminan". Nilai
Diskriminan biasanya dilambangkan dengan Δ atau D. Nilai diskriminan dapat
berupa bilangan riil apa pun (yaitu, positif, negatif, atau 0). Namun dalam artikel
ini kita sepakati diawal akan menggunakan nilai diskriminan menggunakan simbol
D.
Rumus Diskriminan
Diskriminan (D) dari polinomial apa pun dinyatakan
dalam bentuk koefisiennya. Berikut adalah rumus diskriminan untuk persamaan
kubik dan Diskriminan persamaan kuadrat.
1. Jika terdapat persamaan kuadrat ax2 + bx
+ c= 0, maka nilai diskriminannya adalah:
D = b2 - 4ac
2. Jika terdapat persamaan polinomial ax3 +
bx2 + cx + d = 0, maka nilai diskriminannya adalah :
D = b2c2 − 4ac3 − 4b3d
− 27a2d2 + 18abcd
Mari kita lihat cara menggunakan rumus ini untuk
menemukan diskriminan.
Bagaimana Menemukan Diskriminan?
Untuk menemukan diskriminan persamaan kubik atau
persamaan kuadrat, kita hanya perlu membandingkan persamaan yang diberikan
dengan bentuk standarnya dan menentukan koefisiennya terlebih dahulu. Kemudian
kita mengganti koefisien dalam rumus yang relevan untuk menemukan diskriminan.
Diskriminan Persamaan Kuadrat
Diskriminan persamaan kuadrat ax2 + bx + c
= 0 dinyatakan dalam bentuk koefisiennya a, b, dan c. yaitu:
D = b2 − 4ac
Apakah Anda ingat kapan menggunakan b2 −
4ac sebelumnya?
Ya, jawabnya hitungan/rumus tersebut terdapat pada
bagian dari rumus kuadrat dalam menentukan akar-akar persamaan kuadrat:
Di sini, ekspresi yang ada di dalam akar kuadrat rumus kuadrat disebut diskriminan persamaan kuadrat. Rumus kuadrat dalam bentuk diskriminan adalah: :
Perhatikan beberapa contoh berikut.
Tentukan nilai diskriminan dari persamaan-persamaan
kuadrat berikut.
1. x2
+ 3x - 5 = 0
2. x2
- 2x + 6 = 0
3. 2x2
+ 3x - 4 = 0
4. 3x2
- 7x + 5 = 0
Jawaban:
1. Menentukan
diskriminan persamaan kuadrat x2 + 3x - 5 = 0.
Jika persamaan tersebut diselaraskan dengan ax2
+ bx + c = 0, kita peroleh a = 1, b = 3, dan c = -5.
D = b2 − 4ac
= (3)2
- 4(1)(-5)
= 9 + 20
= 29
Jadi, nilai diskriminannya adalah 29.
2. Menentukan
diskriminan persamaan kuadrat x2 - 2x + 6 = 0.
Jika persamaan tersebut diselaraskan dengan ax2
+ bx + c = 0, kita peroleh a = 1, b = -2, dan c = 6.
D = b2 − 4ac
= (-2)2
- 4(1)(6)
= 4 - 24
= -20
Jadi, nilai diskriminannya adalah -20.
3. Menentukan
diskriminan persamaan kuadrat 2x2 + 3x - 4 = 0.
Jika persamaan tersebut diselaraskan dengan ax2
+ bx + c = 0, kita peroleh a = 2, b = 3, dan c = -4.
D = b2 − 4ac
= (3)2
- 4(2)(-4)
= 9 + 32
= 41
Jadi, nilai diskriminannya adalah 41.
4. Menentukan
diskriminan persamaan kuadrat 3x2 - 7x + 5 = 0.
Jika persamaan tersebut diselaraskan dengan ax2
+ bx + c = 0, kita peroleh a = 3, b = -7, dan c = 5.
D = b2 − 4ac
= (-7)2
- 4(3)(5)
= 49 - 60
= -11
Jadi, nilai diskriminannya adalah -11.
Diskriminan Persamaan Kubik
Diskriminan persamaan kubik ax3 + bx2
+ cx + d = 0 dinyatakan dalam suku a, b, c, dan d. yaitu:
D = b2c2 − 4ac3 − 4b3d
− 27a2d2 + 18abcd
Contoh:
Carilah diskriminan persamaan kubik x3 - 3x
+ 2 = 0.
Jika persamaan tersebut diselaraskan dengan ax3
+ bx2 + cx + d = 0, kita peroleh a = 1, b = 0, c = -3, dan d = 2. J
D = b2c2 − 4ac3 − 4b3d
− 27a2d2 + 18abcd
= (0)2(-3)2 − 4(1)(-3)3 − 4(0)3(2) − 27(1)2(2)2 +
18(1)(0)(-3)(2)
= 0 + 108 - 0 - 108 + 0
= 0
Jadi, nilai diskriminannya adalah 0.
Diskriminan dan Sifat Akar
Akar persamaan kuadrat ax2 + bx + c = 0
adalah nilai x yang memenuhi persamaan tersebut. Akar tersebut dapat ditemukan
menggunakan rumus kuadrat:
Meskipun kita tidak dapat menemukan akar hanya dengan
menggunakan diskriminan, kita dapat menentukan sifat-sifat akar sebagai
berikut.
Jika Diskriminan Positif
Jika D > 0 atau b2 − 4ac > 0,
persamaan kuadrat memiliki dua akar riil yang berbeda. Hal ini karena, ketika D
> 0, akar-akar tersebut diberikan oleh:
dan akar kuadrat dari bilangan positif selalu
menghasilkan bilangan riil. Jadi, ketika diskriminan persamaan kuadrat lebih
besar dari 0, persamaan tersebut memiliki dua akar yang merupakan bilangan riil
yang berbeda.
Jika Diskriminan Negatif
Jika D < 0 atau b2 − 4ac < 0, persamaan
kuadrat memiliki dua akar kompleks (akar imajiner) yang berbeda. Hal ini
karena, ketika D < 0, akar-akarnya diberikan oleh
dan akar kuadrat dari bilangan negatif selalu mengarah
ke bilangan imajiner. Misalnya
Jika Diskriminan Sama dengan Nol
Jika D = 0, persamaan kuadrat memiliki dua akar riil yang sama. Dengan kata lain, ketika D = 0, persamaan kuadrat hanya memiliki satu akar riil. Ini karena, ketika D = 0, akar-akarnya diberikan oleh:
dan akar kuadrat dari 0 adalah 0. Maka persamaan
tersebut berubah menjadi x =
Akar persamaan kuadrat tidak lain adalah koordinat-x
dari perpotongan terhadap sumbu X dari fungsi kuadrat. Grafik fungsi kuadrat
dalam dari 3 permasalahan ini dapat digambarkan seperti berikut.
Ketika D > 0, grafik memotong sumbu X di dua titik
koordinat.
Ketika D = 0, grafik memotong sumbu X di satu titik
koordinat (menyinggung)
Ketika D < 0, grafik tidak memotong sumbu X (Tidak memiliki
akar real)
Catatan Penting tentang Diskriminan:
Diskriminan persamaan kuadrat ax2 + bx + c
= 0 adalah Δ atau D = b2 − 4ac.
Persamaan kuadrat dengan diskriminan D memiliki
sifat-sifat akar sebagai berikut.
(i) Dua akar
riil yang tidak sama ketika D > 0.
(ii) Hanya satu akar riil ketika D = 0.
(iii) Tidak ada akar riil atau dua akar kompleks
ketika D < 0.
Perhatikan lagi contoh soal di awal tadi.
Kita akan menentukan sifat-sifat akarnya.
1. x2
+ 3x - 5 = 0, mempunyai nilai diskriminan D = 29 atau D > 0. Berarti
memiliki akar-akar berbeda dan riil.
2. x2
- 2x + 6 = 0, mempunyai nilai diskriminan D = -20 atau D < 0. Berarti
memiliki akar-akar imajiner.
3. 2x2
+ 3x - 4 = 0, mempunyai nilai diskriminan D = 44 atau D > 0. Berarti
memiliki akar-akar berbeda dan riil
4. 3x2
- 7x + 5 = 0, mempunyai nilai diskriminan D = -11 atau D < 0. Berarti
memiliki akar-akar imajiner.
Bagaimana, sudah jelas bukan belajar tentang nilai
Diskriminan?
Demikianlah materi
tentang Diskriminan pada persamaan kuadrat.
Semoga bermanfaat.
Tag:
diskriminan persamaan kuadrat
rumus diskriminan persamaan kuadrat
nilai diskriminan persamaan kuadrat
soal diskriminan persamaan kuadrat kelas 9
nilai diskriminan persamaan kuadrat x2 6x 8 0
nilai diskriminan persamaan kuadrat 2x2 4x 9 0 yaitu
contoh soal diskriminan persamaan kuadrat
nilai diskriminan persamaan kuadrat adalah
jika nilai diskriminan persamaan kuadrat
apa itu diskriminan persamaan kuadrat
nilai diskriminan persamaan kuadrat 5x 4 0 adalah
diskriminan persamaan kuadrat adalah
diskriminan dari persamaan kuadrat adalah
rumus diskriminan persamaan kuadrat adalah



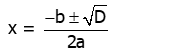





Tidak ada komentar:
Posting Komentar